Kekongruenan dan Kesebangunan

Kekongruenan Bangun Datar

Kongruen adalah keadaan dimana dua bangun datar memiliki ukuran yang sama dan dikatakan sebangun. Dari pengertian tersebut dapat diketahui bahwa semua bangun datar yang kongruen sudah pasti sebangun, namun bangun datar yang sebangun belum tentu kongruen. 

Jadi, ciri-ciri bangun datar yang kongruen adalah :

1. Memiliki panjang sisi yang sama
2. Memiliki bentuk yang sama.
3. Memiliki besar sudut yang sama.
4. Sebangun

Dua bangun segi banyak (poligon) dikatakan kongruen jika memenuhi dua syarat, yaitu :

1. Sisi-sisi yang bersesuaian sama panjang
2. Sudut-sudut yang bersesuaian sama besar

Sudut-sudut yang bersesuaian :

1. Sudut A dan Sudut J ---> Sudut A = Sudut J
2. Sudut B dan Sudut K ---> Sudut B = Sudut K
3. Sudut C dan Sudut M ---> Sudut D = Sudut M

Sisi-sisi yang bersesuaian :

1. AB dan JK ---> AB = JK
2. BC dan KL ---> BC = KL
3. CD dan LM ---> CD = LM
4. DA dan MJ ---> DA = MJ

Kekongruenan Dua Segitiga

Dua bangun yang mempunyai bentuk dan ukuran yang sama dinamakan kongruen. Dua segitiga dikatakan kongruen jika hanya jika memenuhi syarat berikut ini:

1. Sisi-sisi yang bersesuaian sama panjang
2. Sudut-sudut yang bersesuaian sama besar

Sisi-sisi yang bersesuaian:

1. AB dan DE ---> AB = DE
2. BC dan EF ---> BC = EF
3. CA dan FD ---> CA = FD

Sudut-sudut yang bersesuaian:

1. Sudut A dan Sudut D ---> Sudut A = Sudut D
2. Sudut B dan Sudut E ---> Sudut B = Sudut E
3. Sudut C dan Sudut F ---> Sudut C = Sudut F

Kesebangunan Bangun Datar

Kesebangunan bangun datar digunakan untuk membandingkan dua buah bangun datar (atau lebih) dengan bentuk yang sama. Dua buah bangun datar dapat dikatakan sebangun apabila panjang setiap sisi pada kedua bangun datar tersebut memiliki nilai perbandingan yang sama.

Tidak perlu ukurannya sama, tetapi sisi-sisi yang bersesuaian sebanding (proportional) dan sudut-sudut yang bersesuaian sama besar. Perubahan bangun satu menjadi bangun lain yang sebangun melibatkan perbesaran atau pengecilan. Dengan kata lain dua bangun dikatakan sebangun jika memenuhi syarat:

Perbandingan panjang sisi yang bersesuaian senilai

 

Sudut yang bersesuaian besarnya sama

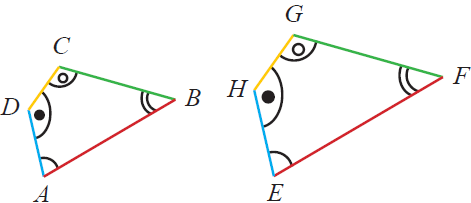
1. Sudut mA = Sudut mE
2. Sudut mB = Sudut mF
3. Sudut mC = Sudut mG
4. Sudut mD = Sudut mH

Kesebangunan Dua Segitiga

Dua segitiga dikatakan sebangun jika hanya jika memenuhi syarat berikut ini:

1. Perbandingan sisi-sisi yang bersesuaian senilai
2. Besar sudut-sudut yang bersesuaian sama

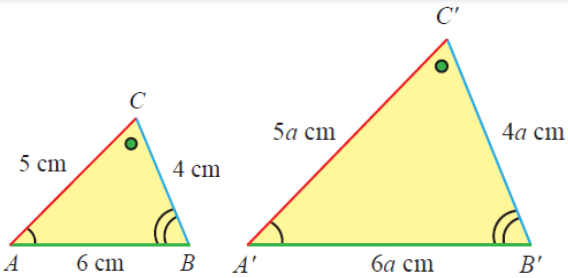
Perbandingan sisi-sisi yang bersesuaian senilai

Besar sudut-sudut yang bersesuaian sama